使用实时示波器进行FFT分析的六大原则
我们生活在时域中。这是我们衡量所有数字性能的地方。但有时，我们可以通过绕道频域来更快地得到答案。通过六个原理，我们可以了解示波器如何将时域测量转换为频域视图。所有六种原理均由具有快速傅里叶变换 （FFT） 功能的示波器“在引擎盖下”应用。
1. 频谱是正弦波分量的组合
在频域中，我们唯一可以考虑的波形是正弦波。还有其他特殊波形，其组合可以描述任何时域波形，例如勒让德多项式、Hermite 多项式，甚至小波，但我们挑出正弦波作为频域描述的原因是正弦波是二阶、线性和微分方程的解——这些方程在涉及电阻器的电路中经常出现， 电容器和电感元件。这意味着，当使用正弦波组合时，与RLC电路产生或相互作用的信号描述比任何其他功能都更简单，因为正弦波自然会发生。
由示波器测量的正弦波在采集缓冲器（图1）中具有<>万个电压时间[V（t）]数据点，在频域中仅用三个数字描述：频率值、幅度值和相位值。这是对原始复杂波形的显着简化。
图1.时域中的100 MHz正弦波及其频域中的频谱显示了100 MHz处的一个峰值。
2. 无限地将波形附加到自身上，创建周期性波形
当我们在时域中获取波形并将其转换为频域时，我们最终会得到一组正弦波，每个正弦波都有一个频率值、一个幅度和一个相位。在时域中，我们将测量描述为具有总采集时间T和样本之间的时间间隔△T的采集缓冲区。当我们在频域中描述相同的波形时，我们将所有正弦波分量的集合（每个分量都有频率、幅度和相位）称为频谱。
不幸的是，我们只能在周期性的V（t）波形上使用离散傅立叶变换（DFT）。如果它不是周期性的，我们必须人为地使它周期性。我们用来将测量数据的任何任意采集缓冲器转换为周期波形的技巧是获取总时间T的采集缓冲器，并在过去永远重复它，在将来永远重复它。
当我们有这种人为重复的波形时，我们可以应用DFT的功率来数学计算频谱中的每个频率分量。以下是用于计算每个频率分量的幅度和相位的公式：
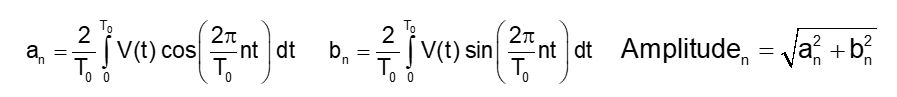
这些积分在频谱中创建某些特征。
3. 频谱中仅出现离散频率;最低是根本的
在计算的频谱中，仅显示离散频率值。最低频率分量称为基波。它是我们可以放入采集缓冲时间的最低频率正弦波。这个最低频率正弦波的周期P是总采集时间T。
由于P等于T，基频为：
频谱中的每个频率分量的频率仅为基波的整数倍：
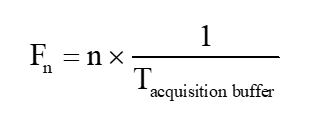
基波的倍数是我们将在频谱中看到的唯一频率分量。这意味着，每个频率分量之间的频率间隔或分辨率是基频。如果我们想要更高的分辨率来区分频谱中间隔较近的频率特征，我们需要在示波器中使用更长的采集时间。
4.最高频率是奈奎斯特，或采样率的一半
频谱中的最高频率分量与缓冲区中采样点之间的时间间隔有关。至少，我们需要在一个周期内测量两个V（t）点来计算该频率分量的幅度和相位的值。这意味着我们可以计算的最高频率正弦波的周期是时间间隔的两倍，或Pmax = 2 x △T。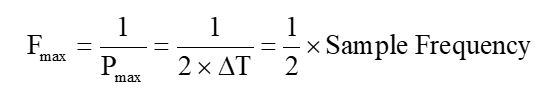
频谱中最高的频率分量也称为奈奎斯特频率。由于获取数据的采样率为奈奎斯特频率1/△T，因此我们可以计算正弦波分量的最高频率是采样率的一半。如果采样率为 10 GS/s，则奈奎斯特频率为 5 GHz。
理想正弦波的平均值始终为 0。这意味着，当我们使用一组正弦波来描述真实波形时，重新创建的时域波形的平均值始终为0。但实际波形具有平均值或直流偏移。为了解决这个问题，我们将直流分量存储在0 Hz频率分量中，这是0 x基波。在大多数示波器中，您可以抑制绘制 0千频率分量以放大显示器的比例。
5. FFT 通过首先将缓冲区截断为 2^n 个采样点来加快计算速度
一百万个数据点将涉及大约一万亿次DFT计算来创建一个频谱。这可能需要比方便更长的时间来计算。为了解决这个问题，我们使用称为FFT的DFT的更快版本。它计算与 DFT 相同的积分，但它应用矩阵数学来使用点总数为 2 的幂来执行计算。如果缓冲区中有 2 万个点，则 FFT 计算中可以包含的最大点数为 19^524 = 288，<> 个点。我们丢弃了几乎一半的测量数据，以获得令人难以置信的快速计算时间。
执行FFT的第一步是定义采集缓冲区的区域，该区域包含将要计算的最大数量的2^n点。大多数示波器允许您选择时域屏幕的中心区域或从左边缘计数。图2显示了FFT计算中将包括的虚线之间的区域。
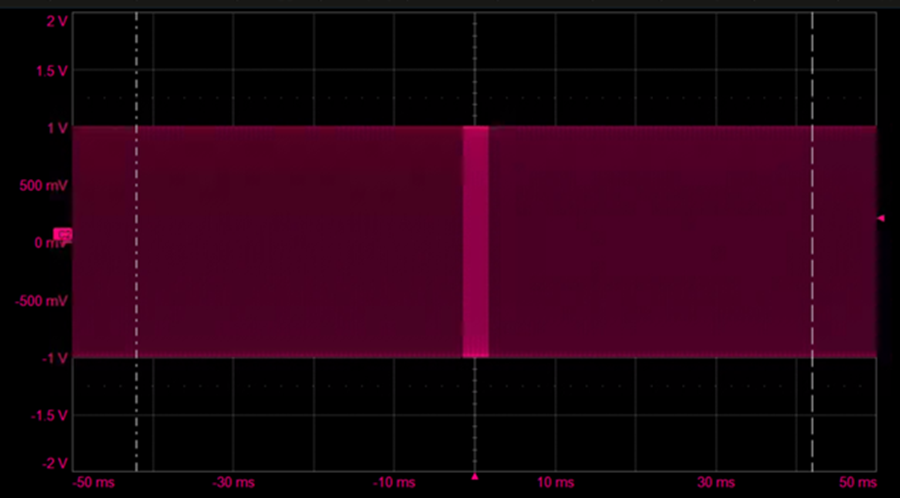图2.垂直虚线之间是采集缓冲区的区域，其中包含将在FFT中使用的2^n点。
当采集缓冲时间为1 μs，并且我们有1万个点时，我们预计基波为1 MHz。在频谱中，FFT采集缓冲器小于此值，这意味着实际分辨率略大于<> MHz。但是，在考虑频谱特征时，这些估计仍然是一个很好的价值。
6. 窗口功能可防止因截断而导致的光谱泄漏
为了创建周期波形，我们采用采集缓冲器并无限期地重复它。使用 FFT 函数时，我们进一步截断了采集缓冲区，并无限期地重复截断的缓冲区。这意味着在每个附加采集缓冲器的边界处，对应于一个缓冲器的结尾和下一个缓冲器的开始的波形可能存在不连续性（图 3）。
图3.在采集缓冲器中没有整数个周期的正弦波信号示例。当相互附加时，缓冲器每个边缘的波形都有一个不连续性，由NI提供。
通常，在每个缓冲器中具有整数周期数的正弦波的频谱在其峰值频率处将具有单个频率尖峰。但是，如果由于截断的采集缓冲器而人为地切断了正弦波，则无限长的波形现在将具有不连续性，这将迫使峰值频率中的一些频率分量进入相邻的频率分量，这可能导致窄峰值失真。
这种效应称为光谱泄漏。这是由于第一个电压值与最后一个电压值不同而导致缓冲器边界处不连续性的伪影。减少此伪影的方法是通过将整个采集缓冲区乘以窗口函数来人为地减少不连续性。这会逐渐强制采集缓冲器末端的电压值为0，从而保证一个缓冲器的末端与下一个缓冲器的开头连续。
有许多常用的窗口函数。它们的不同之处在于它们允许的光谱泄漏量和由此产生的分辨率。除非您有充分的理由，否则我们建议您始终使用 von Hann（有时称为 Hanning）或 Blackman-Harris 函数。
分析频域中的时域波形
频谱分析的价值在于能够识别重复信号的频谱“指纹”，其频率在基波（1/采集缓冲器）和奈奎斯特（<>/<> x采样率）之间的范围内。每次示波器测量新的时域电压采集缓冲器时，都会显示新计算的频谱响应。随着源中的周期性信号发生变化，它们的光谱指纹也会发生变化。
任何可能有助于识别给定频率的周期信号的应用都是实时频谱分析的绝佳候选者。最常见的应用是搜索重要信号的干扰源。图4显示了开关模式电源（SMPS）负载变化时输出的频谱响应。峰值约为50 kHz，开关频率随负载变化而随时间变化，如图上部的频谱图所示。当您在这些频率分量中观察放大器的噪声或振荡器的抖动时，您就会知道可能的根本原因。
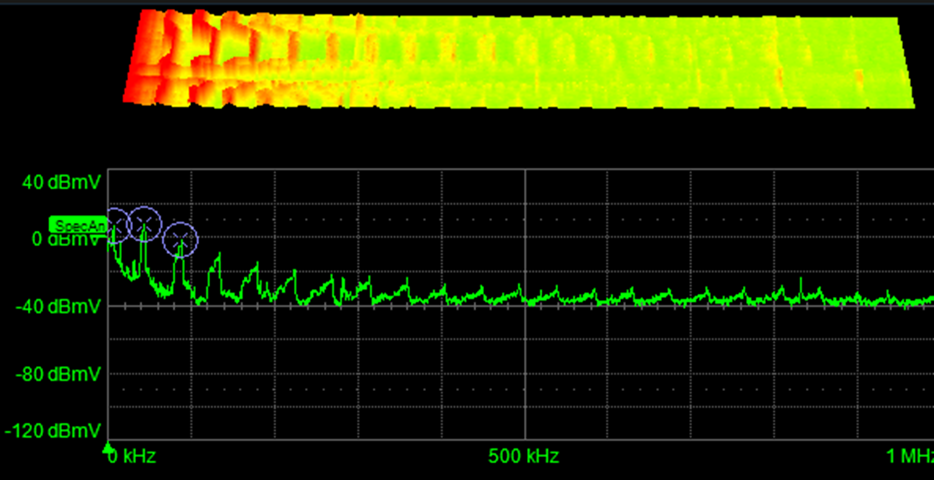图4.输出负载变化时SMPS输出的实时频谱示例，显示了峰值频率的时间变化。
在查看RF干扰频谱时，我们通常可以拾取特定的通信信号。图5显示了使用带有大尖端环路的10倍探头测量的USB供电设备中电源轨的实时频谱。频谱指纹显示从87 MHz到108 MHz的FM无线电频段的拾音。
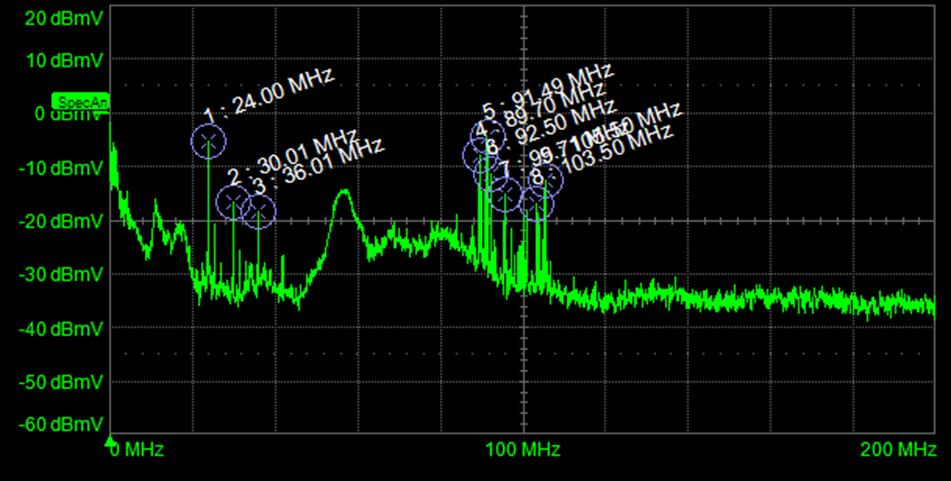图5.测量的USB电源轨噪声的实时频谱，显示探头拾取的FM无线电频段中的大型分量。
我们生活在时域中。这是我们衡量所有数字性能的地方。但有时，我们可以通过绕道频域来更快地得到答案。通过六个原理，我们可以了解示波器如何将时域测量转换为频域视图。所有六种原理均由具有快速傅里叶变换 （FFT） 功能的示波器“在引擎盖下”应用。
1. 频谱是正弦波分量的组合
在频域中，我们唯一可以考虑的波形是正弦波。还有其他特殊波形，其组合可以描述任何时域波形，例如勒让德多项式、Hermite 多项式，甚至小波，但我们挑出正弦波作为频域描述的原因是正弦波是二阶、线性和微分方程的解——这些方程在涉及电阻器的电路中经常出现， 电容器和电感元件。这意味着，当使用正弦波组合时，与RLC电路产生或相互作用的信号描述比任何其他功能都更简单，因为正弦波自然会发生。
由示波器测量的正弦波在采集缓冲器（图1）中具有<>万个电压时间[V（t）]数据点，在频域中仅用三个数字描述：频率值、幅度值和相位值。这是对原始复杂波形的显着简化。
图1.时域中的100 MHz正弦波及其频域中的频谱显示了100 MHz处的一个峰值。
2. 无限地将波形附加到自身上，创建周期性波形
当我们在时域中获取波形并将其转换为频域时，我们最终会得到一组正弦波，每个正弦波都有一个频率值、一个幅度和一个相位。在时域中，我们将测量描述为具有总采集时间T和样本之间的时间间隔△T的采集缓冲区。当我们在频域中描述相同的波形时，我们将所有正弦波分量的集合（每个分量都有频率、幅度和相位）称为频谱。
不幸的是，我们只能在周期性的V（t）波形上使用离散傅立叶变换（DFT）。如果它不是周期性的，我们必须人为地使它周期性。我们用来将测量数据的任何任意采集缓冲器转换为周期波形的技巧是获取总时间T的采集缓冲器，并在过去永远重复它，在将来永远重复它。
当我们有这种人为重复的波形时，我们可以应用DFT的功率来数学计算频谱中的每个频率分量。以下是用于计算每个频率分量的幅度和相位的公式：
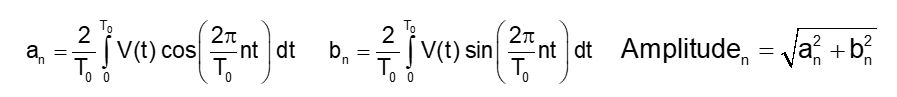
这些积分在频谱中创建某些特征。
3. 频谱中仅出现离散频率;最低是根本的
在计算的频谱中，仅显示离散频率值。最低频率分量称为基波。它是我们可以放入采集缓冲时间的最低频率正弦波。这个最低频率正弦波的周期P是总采集时间T。
由于P等于T，基频为：
频谱中的每个频率分量的频率仅为基波的整数倍：
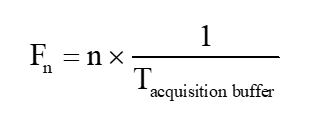
基波的倍数是我们将在频谱中看到的唯一频率分量。这意味着，每个频率分量之间的频率间隔或分辨率是基频。如果我们想要更高的分辨率来区分频谱中间隔较近的频率特征，我们需要在示波器中使用更长的采集时间。
4.最高频率是奈奎斯特，或采样率的一半
频谱中的最高频率分量与缓冲区中采样点之间的时间间隔有关。至少，我们需要在一个周期内测量两个V（t）点来计算该频率分量的幅度和相位的值。这意味着我们可以计算的最高频率正弦波的周期是时间间隔的两倍，或Pmax = 2 x △T。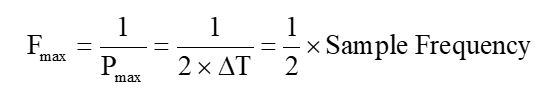
频谱中最高的频率分量也称为奈奎斯特频率。由于获取数据的采样率为奈奎斯特频率1/△T，因此我们可以计算正弦波分量的最高频率是采样率的一半。如果采样率为 10 GS/s，则奈奎斯特频率为 5 GHz。
理想正弦波的平均值始终为 0。这意味着，当我们使用一组正弦波来描述真实波形时，重新创建的时域波形的平均值始终为0。但实际波形具有平均值或直流偏移。为了解决这个问题，我们将直流分量存储在0 Hz频率分量中，这是0 x基波。在大多数示波器中，您可以抑制绘制 0千频率分量以放大显示器的比例。
5. FFT 通过首先将缓冲区截断为 2^n 个采样点来加快计算速度
一百万个数据点将涉及大约一万亿次DFT计算来创建一个频谱。这可能需要比方便更长的时间来计算。为了解决这个问题，我们使用称为FFT的DFT的更快版本。它计算与 DFT 相同的积分，但它应用矩阵数学来使用点总数为 2 的幂来执行计算。如果缓冲区中有 2 万个点，则 FFT 计算中可以包含的最大点数为 19^524 = 288，<> 个点。我们丢弃了几乎一半的测量数据，以获得令人难以置信的快速计算时间。
执行FFT的第一步是定义采集缓冲区的区域，该区域包含将要计算的最大数量的2^n点。大多数示波器允许您选择时域屏幕的中心区域或从左边缘计数。图2显示了FFT计算中将包括的虚线之间的区域。
图2.垂直虚线之间是采集缓冲区的区域，其中包含将在FFT中使用的2^n点。
当采集缓冲时间为1 μs，并且我们有1万个点时，我们预计基波为1 MHz。在频谱中，FFT采集缓冲器小于此值，这意味着实际分辨率略大于<> MHz。但是，在考虑频谱特征时，这些估计仍然是一个很好的价值。
6. 窗口功能可防止因截断而导致的光谱泄漏
为了创建周期波形，我们采用采集缓冲器并无限期地重复它。使用 FFT 函数时，我们进一步截断了采集缓冲区，并无限期地重复截断的缓冲区。这意味着在每个附加采集缓冲器的边界处，对应于一个缓冲器的结尾和下一个缓冲器的开始的波形可能存在不连续性（图 3）。
图3.在采集缓冲器中没有整数个周期的正弦波信号示例。当相互附加时，缓冲器每个边缘的波形都有一个不连续性，由NI提供。
通常，在每个缓冲器中具有整数周期数的正弦波的频谱在其峰值频率处将具有单个频率尖峰。但是，如果由于截断的采集缓冲器而人为地切断了正弦波，则无限长的波形现在将具有不连续性，这将迫使峰值频率中的一些频率分量进入相邻的频率分量，这可能导致窄峰值失真。
这种效应称为光谱泄漏。这是由于第一个电压值与最后一个电压值不同而导致缓冲器边界处不连续性的伪影。减少此伪影的方法是通过将整个采集缓冲区乘以窗口函数来人为地减少不连续性。这会逐渐强制采集缓冲器末端的电压值为0，从而保证一个缓冲器的末端与下一个缓冲器的开头连续。
有许多常用的窗口函数。它们的不同之处在于它们允许的光谱泄漏量和由此产生的分辨率。除非您有充分的理由，否则我们建议您始终使用 von Hann（有时称为 Hanning）或 Blackman-Harris 函数。
分析频域中的时域波形
频谱分析的价值在于能够识别重复信号的频谱“指纹”，其频率在基波（1/采集缓冲器）和奈奎斯特（<>/<> x采样率）之间的范围内。每次示波器测量新的时域电压采集缓冲器时，都会显示新计算的频谱响应。随着源中的周期性信号发生变化，它们的光谱指纹也会发生变化。
任何可能有助于识别给定频率的周期信号的应用都是实时频谱分析的绝佳候选者。最常见的应用是搜索重要信号的干扰源。图4显示了开关模式电源（SMPS）负载变化时输出的频谱响应。峰值约为50 kHz，开关频率随负载变化而随时间变化，如图上部的频谱图所示。当您在这些频率分量中观察放大器的噪声或振荡器的抖动时，您就会知道可能的根本原因。
图4.输出负载变化时SMPS输出的实时频谱示例，显示了峰值频率的时间变化。
在查看RF干扰频谱时，我们通常可以拾取特定的通信信号。图5显示了使用带有大尖端环路的10倍探头测量的USB供电设备中电源轨的实时频谱。频谱指纹显示从87 MHz到108 MHz的FM无线电频段的拾音。
图5.测量的USB电源轨噪声的实时频谱，显示探头拾取的FM无线电频段中的大型分量。